三维张量→Attention机制：线性代数如何成为大模型的架构蓝图

本文较长，建议点赞收藏，以免遗失。更多AI大模型应用开发学习内容和资料尽在AI大模型技术社公众号。

一、向量：高维空间的数据载体

物理意义：带方向的量，AI中表示特征/词嵌入
核心操作：

import numpy as np

# 向量创建与运算
v1 = np.array([2, 5, -1])  # 3维向量
v2 = np.array([-1, 3, 4])
print("点积:", np.dot(v1, v2))       # 输出：2*(-1)+5*3+(-1)*4=9
print("L2范数:", np.linalg.norm(v1)) # 输出：√(4+25+1)≈5.48

二、矩阵：神经网络的基础结构

核心作用：

• 全连接层权重：W ∈ ℝ^(m×n)
• 图像数据：[height, width, channels]
• 注意力分数：A = QK^T/√d_k

矩阵分解示例：

# 矩阵特征分解
A = np.array([[4, 1], [1, 3]])
eigvals, eigvecs = np.linalg.eig(A)
print("特征值:", eigvals)    # 输出：[4.618, 2.382]
print("特征向量:\n", eigvecs) # 正交基向量

三、张量：多维数据的统一表示

AI中的应用：

import torch

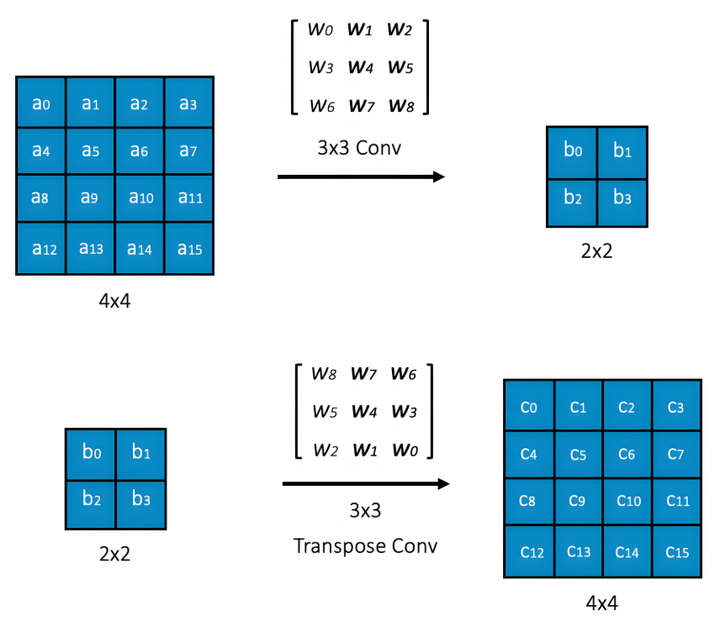
# 创建3维张量 (batch_size, seq_len, hidden_dim)
tensor = torch.randn(32, 128, 768)  # BERT隐藏层典型维度

# 张量运算 (矩阵乘法扩展)
A = torch.randn(32, 128, 50)
B = torch.randn(32, 50, 768)
C = torch.matmul(A, B)  # 输出维度: (32, 128, 768)

四、矩阵运算：模型计算的引擎

关键操作与复杂度：

GPU加速实践：

# 比较CPU/GPU矩阵运算速度
import time

n = 4096  # 大模型常见维度

# CPU计算
A_cpu = torch.randn(n, n)
B_cpu = torch.randn(n, n)
start = time.time()
C_cpu = A_cpu @ B_cpu
print(f"CPU耗时: {time.time()-start:.4f}s")

# GPU计算
A_gpu = A_cpu.cuda()
B_gpu = B_cpu.cuda()
torch.cuda.synchronize()
start = time.time()
C_gpu = A_gpu @ B_gpu
torch.cuda.synchronize()
print(f"GPU耗时: {time.time()-start:.4f}s")

典型输出：CPU耗时 1.2s, GPU耗时 0.05s (加速24倍)

五、特征值分解：模型稳定性分析

应用场景：

• 优化器步长确定（Hessian矩阵特征值）
• PCA降维（协方差矩阵分解）
• PageRank算法（随机矩阵分析）

病态矩阵示例：

# 条件数 = 最大特征值/最小特征值
A = np.array([[1000, 0.001], [0.001, 0.001]])
cond_num = np.linalg.cond(A)
print("条件数:", cond_num)  # 输出约1e6，极端病态矩阵

# 小扰动导致大误差
b = np.array([1, 0.001])
x_true = np.linalg.solve(A, b)
A_perturb = A + np.random.randn(2,2)*1e-3
x_perturb = np.linalg.solve(A_perturb, b)
error = np.linalg.norm(x_true - x_perturb)
print(f"扰动后误差: {error:.2f}")  # 误差可达数百倍

六、奇异值分解（SVD）：模型压缩核心技术

数学表达：
A = UΣVᵀ，其中：

• U：左奇异向量（行空间基）
• Σ：奇异值对角阵（重要性排序）
• V：右奇异向量（列空间基）

模型压缩实战：

# 全连接层权重压缩
W = torch.randn(4096, 4096)  # 原始权重

# SVD分解
U, S, Vt = torch.linalg.svd(W)

# 保留前k个奇异值 (压缩率= k*(m+n)/m/n)
k = 1024  # 75%压缩率
W_compressed = U[:, :k] @ torch.diag(S[:k]) @ Vt[:k, :]

# 验证重构误差
error = torch.norm(W - W_compressed) / torch.norm(W)
print(f"重构相对误差: {error:.4f}")  # 典型值 <0.05

七、大模型中的线性代数应用

Transformer关键运算：

# 自注意力机制核心代码 (简化版)
def self_attention(Q, K, V):
    """
    Q: 查询向量 [batch, seq_len, d_k]
    K: 键向量   [batch, seq_len, d_k]
    V: 值向量   [batch, seq_len, d_v]
    """
    scores = torch.matmul(Q, K.transpose(-2, -1)) / np.sqrt(d_k)
    attn_weights = torch.softmax(scores, dim=-1)
    return torch.matmul(attn_weights, V)  # 输出 [batch, seq_len, d_v]

数学本质：

Attention(Q,K,V) = softmax(QKᵀ/√dₖ)V

本质是矩阵乘法+概率归一化

八、高效计算技巧

避免常见性能陷阱：

# 低效实现 (逐元素操作)
output = torch.zeros_like(input)
for i in range(rows):
    for j in range(cols):
        output[i,j] = input[i,j] * weight[j]  # O(n²)复杂度

# 高效实现 (广播机制)
output = input * weight.unsqueeze(0)  # O(1)隐式扩展

内存优化实践：

# 原地操作减少内存分配
x = torch.rand(10000, 10000)
y = torch.rand(10000, 10000)

# 常规操作 (额外分配内存)
z = x + y  # 分配新内存

# 原地操作 (节省50%内存)
x.add_(y)  # 结果直接存入x

九、学习路线与资源

知识图谱：

graph LR
    A[向量空间] --> B[矩阵运算]
    B --> C[特征分解]
    C --> D[SVD]
    D --> E[张量微积分]
    E --> F[自动微分]
    F --> G[大模型架构]

十、核心要义总结

向量是特征表示原子单位

• • 词向量：glove = [0.2, -1.3, ..., 0.8] ∈ R^300
  • 位置编码：PE(pos,2i)=sin(pos/10000^(2i/d_model))

矩阵运算是模型计算骨架

• • 单层计算量：FLOPs = 2 × in_dim × out_dim

SVD实现模型压缩与加速

• • LLAMA-2 70B参数压缩：奇异值保留率>95%时，压缩比可达4:1

特征值揭示模型优化特性

• • 损失函数Hessian矩阵最大特征值决定最优学习率：η < 2/λ_max

大模型本质是高维张量的复合函数。当理解每一行代码背后的数学意义，你便从调参者蜕变为模型架构师。更多AI大模型应用开发学习内容和资料，尽在AI大模型技术社公众号。